Mục lục
- 1. Giới Thiệu: Độ Dốc Là Gì và Tại Sao Nó Quan Trọng?
- 2. Làm Thế Nào Để Tính Độ Dốc?
- 3. Các Loại Độ Dốc Phổ Biến
- 4. Ứng Dụng Thực Tế Của Độ Dốc
- 5. Những Lưu Ý và Sai Lầm Thường Gặp
- 6. Kết Luận
1. Giới Thiệu: Độ Dốc Là Gì và Tại Sao Nó Quan Trọng?
Trong thế giới toán học và vật lý, khái niệm “độ dốc” (slope) xuất hiện ở khắp mọi nơi, từ những đường thẳng đơn giản trên đồ thị đến việc mô tả độ nghiêng của một con đường hay tốc độ thay đổi của một đại lượng nào đó. Hiểu một cách đơn giản, độ dốc là thước đo độ nghiêng hoặc độ dốc của một đường thẳng. Nó cho chúng ta biết một đường thẳng “dốc” như thế nào và theo hướng nào (lên hay xuống khi di chuyển từ trái sang phải).
Tại sao độ dốc lại quan trọng? Nó không chỉ là một khái niệm trừu tượng trong sách giáo khoa. Độ dốc có vô số ứng dụng thực tế:
- Kỹ thuật và Xây dựng: Xác định độ nghiêng mái nhà, độ dốc đường đi, đường ống thoát nước để đảm bảo an toàn và hiệu quả.
- Kinh tế học: Phân tích tốc độ tăng trưởng doanh thu, chi phí, lợi nhuận qua thời gian (ví dụ: đường cung, đường cầu).
- Vật lý: Mô tả vận tốc (độ dốc của đồ thị quãng đường-thời gian) hoặc gia tốc (độ dốc của đồ thị vận tốc-thời gian).
- Địa lý và Bản đồ học: Biểu thị độ dốc của địa hình, ảnh hưởng đến dòng chảy sông ngòi, quy hoạch sử dụng đất.
- Thống kê: Đường hồi quy tuyến tính sử dụng độ dốc để mô tả mối quan hệ giữa các biến số.
Nắm vững khái niệm độ dốc không chỉ giúp bạn giải quyết các bài toán trong lớp học mà còn cung cấp một công cụ mạnh mẽ để hiểu và phân tích thế giới xung quanh. Hãy cùng đi sâu vào cách tính và các loại độ dốc khác nhau.
2. Làm Thế Nào Để Tính Độ Dốc?
Có hai cách chính để hình dung và tính toán độ dốc của một đường thẳng trên mặt phẳng tọa độ (Cartesian plane).
2.1. Khái niệm ‘Rise over Run’ (Độ cao trên Độ dài)
Đây là cách trực quan nhất để hiểu về độ dốc. Hãy tưởng tượng bạn đang di chuyển dọc theo đường thẳng từ một điểm này đến điểm khác.
- Rise (Độ thay đổi theo chiều dọc): Là sự thay đổi về tung độ (trục y) giữa hai điểm. Nếu bạn đi lên, ‘rise’ là dương. Nếu bạn đi xuống, ‘rise’ là âm.
- Run (Độ thay đổi theo chiều ngang): Là sự thay đổi về hoành độ (trục x) giữa hai điểm, luôn tính từ trái sang phải. Do đó, ‘run’ thường là dương.
Độ dốc chính là tỷ lệ giữa ‘rise’ và ‘run’:
Độ dốc = Rise / Run
Ví dụ, nếu bạn di chuyển lên 3 đơn vị (rise = 3) và sang phải 2 đơn vị (run = 2), độ dốc sẽ là 3/2.
2.2. Công Thức Tính Độ Dốc Chính Xác
Để tính toán chính xác hơn, đặc biệt khi bạn biết tọa độ của hai điểm bất kỳ trên đường thẳng, chúng ta sử dụng công thức toán học. Giả sử chúng ta có hai điểm A(x1, y1) và B(x2, y2) trên đường thẳng.
- Sự thay đổi theo chiều dọc (Rise) là: Δy = y2 – y1
- Sự thay đổi theo chiều ngang (Run) là: Δx = x2 – x1
Công thức tính độ dốc (thường ký hiệu là ‘m’) là:
m = Δy / Δx = (y2 – y1) / (x2 – x1)
Lưu ý quan trọng: Bạn phải giữ nguyên thứ tự trừ của các tọa độ (nếu lấy y2 trừ y1 thì phải lấy x2 trừ x1). Và điều kiện là x1 phải khác x2 (tức là Δx ≠ 0). Trường hợp x1 = x2 sẽ được xét ở phần độ dốc không xác định.

3. Các Loại Độ Dốc Phổ Biến
Dựa vào giá trị tính được, độ dốc của một đường thẳng có thể rơi vào một trong bốn trường hợp chính:
3.1. Độ Dốc Dương (Positive Slope)
- Đặc điểm: Đường thẳng đi lên từ trái sang phải.
- Giá trị: m > 0.
- Ý nghĩa: Khi giá trị x tăng, giá trị y cũng tăng. ‘Rise’ và ‘Run’ cùng dấu (thường là cả hai cùng dương khi di chuyển từ trái sang phải).
- Ví dụ: Một đường thẳng đi qua điểm (1, 2) và (3, 6). Độ dốc m = (6 – 2) / (3 – 1) = 4 / 2 = 2.
3.2. Độ Dốc Âm (Negative Slope)
- Đặc điểm: Đường thẳng đi xuống từ trái sang phải.
- Giá trị: m < 0.
- Ý nghĩa: Khi giá trị x tăng, giá trị y lại giảm. ‘Rise’ và ‘Run’ trái dấu (khi di chuyển từ trái sang phải, ‘Run’ dương nhưng ‘Rise’ âm).
- Ví dụ: Một đường thẳng đi qua điểm (-1, 5) và (2, -1). Độ dốc m = (-1 – 5) / (2 – (-1)) = -6 / 3 = -2.
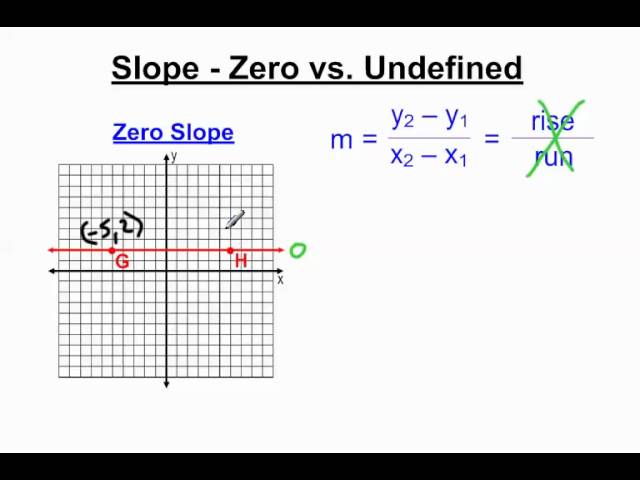
3.3. Độ Dốc Bằng Không (Zero Slope)
- Đặc điểm: Đường thẳng nằm ngang, song song với trục x.
- Giá trị: m = 0.
- Ý nghĩa: Giá trị y không thay đổi khi x thay đổi. ‘Rise’ bằng 0 (y2 – y1 = 0).
- Ví dụ: Một đường thẳng đi qua điểm (2, 4) và (5, 4). Độ dốc m = (4 – 4) / (5 – 2) = 0 / 3 = 0. Tất cả các điểm trên đường thẳng này đều có tung độ là 4 (phương trình y = 4).
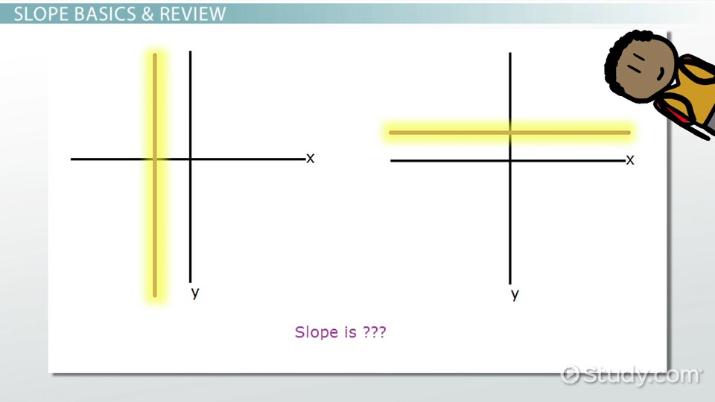
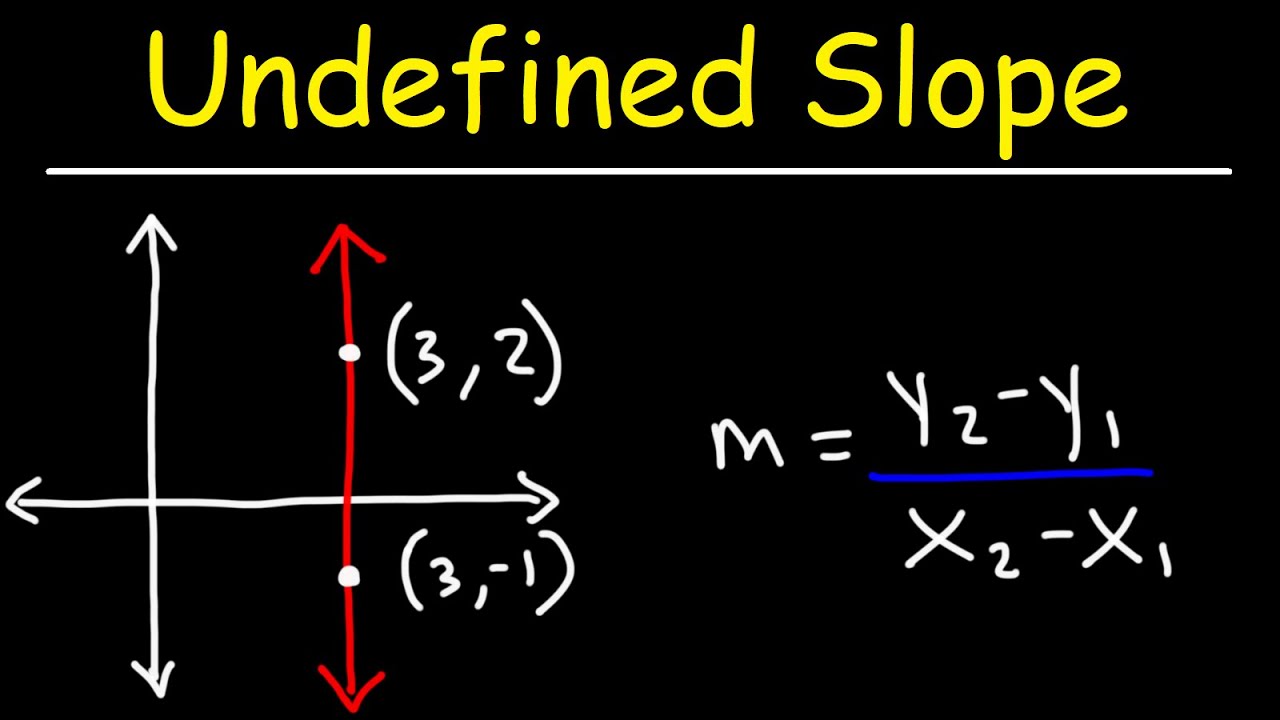
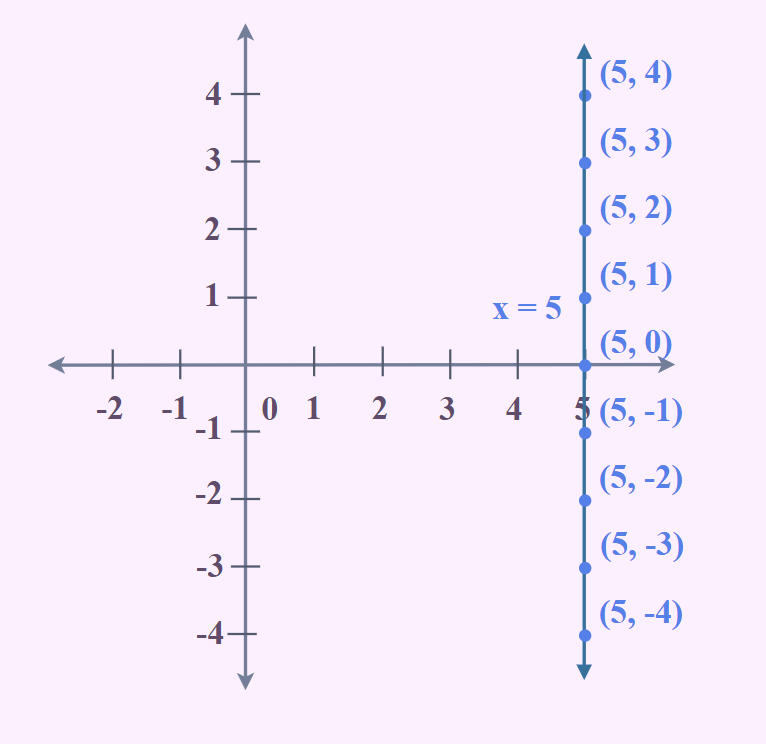
3.4. Độ Dốc Không Xác Định (Undefined Slope)
- Đặc điểm: Đường thẳng thẳng đứng, song song với trục y.
- Giá trị: Không xác định (Undefined).
- Ý nghĩa: Giá trị x không thay đổi, tất cả các điểm trên đường thẳng có cùng hoành độ. ‘Run’ bằng 0 (x2 – x1 = 0). Vì phép chia cho 0 không xác định trong toán học, nên độ dốc cũng không xác định.
- Ví dụ: Một đường thẳng đi qua điểm (3, 1) và (3, 5). Khi tính độ dốc, ta có (5 – 1) / (3 – 3) = 4 / 0. Phép chia cho 0 là không hợp lệ. Tất cả các điểm trên đường thẳng này đều có hoành độ là 3 (phương trình x = 3).

4. Ứng Dụng Thực Tế Của Độ Dốc
Như đã đề cập, độ dốc không chỉ tồn tại trên giấy. Nó là một công cụ mô tả thế giới thực mạnh mẽ:
- Trong xây dựng đường bộ: Các kỹ sư tính toán độ dốc của đường để đảm bảo thoát nước tốt, an toàn cho xe cộ khi lên và xuống dốc. Độ dốc quá lớn có thể nguy hiểm, đặc biệt trong điều kiện thời tiết xấu.
- Trong thiết kế kiến trúc: Độ dốc mái nhà ảnh hưởng đến việc thoát nước mưa, tuyết và cả tính thẩm mỹ của công trình. Độ dốc của đường dốc cho người khuyết tật phải tuân theo các tiêu chuẩn nghiêm ngặt để đảm bảo khả năng tiếp cận.
- Trong kinh doanh và tài chính: Các nhà phân tích sử dụng độ dốc của đường xu hướng trên biểu đồ để dự đoán doanh số, lợi nhuận hoặc giá cổ phiếu. Độ dốc dương cho thấy sự tăng trưởng, độ dốc âm cho thấy sự suy giảm.
- Trong khoa học máy tính: Các thuật toán tối ưu hóa như Gradient Descent sử dụng khái niệm độ dốc (gradient – đạo hàm riêng, một dạng tổng quát của độ dốc) để tìm giá trị cực tiểu hoặc cực đại của một hàm mục tiêu.
- Trong thể thao: Phân tích độ dốc của đường chạy, đường đua xe đạp giúp vận động viên điều chỉnh chiến thuật và sức lực.
Việc hiểu rõ độ dốc giúp chúng ta đưa ra quyết định tốt hơn trong nhiều lĩnh vực, từ việc chọn con đường đi bộ ít dốc nhất đến việc đánh giá hiệu quả của một chiến lược kinh doanh.
5. Những Lưu Ý và Sai Lầm Thường Gặp
Khi làm việc với độ dốc, có một số điểm cần lưu ý để tránh nhầm lẫn:
- Thứ tự các điểm: Khi dùng công thức m = (y2 – y1) / (x2 – x1), hãy đảm bảo bạn trừ tọa độ y và x theo cùng một thứ tự (điểm 2 trừ điểm 1 hoặc điểm 1 trừ điểm 2). Nếu bạn đảo ngược thứ tự ở tử số mà không đảo ngược ở mẫu số (hoặc ngược lại), bạn sẽ nhận được kết quả sai dấu.
- Phân biệt độ dốc bằng không và không xác định: Đây là lỗi phổ biến. Đường nằm ngang có độ dốc bằng 0 (Zero Slope), trong khi đường thẳng đứng có độ dốc không xác định (Undefined Slope). Đừng nhầm lẫn chúng!
- Đơn vị: Trong các ứng dụng thực tế, hãy chú ý đến đơn vị của trục y và trục x. Độ dốc sẽ có đơn vị là (đơn vị của y) / (đơn vị của x). Ví dụ, nếu y là mét và x là giây, độ dốc sẽ có đơn vị là mét/giây (đơn vị của vận tốc).
- Độ dốc và góc nghiêng: Độ dốc (m) và góc nghiêng (θ, góc tạo bởi đường thẳng và phương ngang) có liên quan qua hàm tang: m = tan(θ). Tuy nhiên, chúng không giống nhau. Độ dốc có thể là bất kỳ số thực nào, trong khi góc nghiêng thường được đo bằng độ hoặc radian.
- Đường cong: Khái niệm độ dốc cơ bản này áp dụng cho đường thẳng. Đối với đường cong, độ dốc tại một điểm cụ thể được xác định bằng độ dốc của đường tiếp tuyến tại điểm đó, và đây là khái niệm cơ bản của đạo hàm trong giải tích.
6. Kết Luận
Độ dốc là một khái niệm toán học nền tảng nhưng vô cùng mạnh mẽ và hữu ích. Từ việc mô tả hình dạng của một đường thẳng đơn giản đến việc phân tích các xu hướng phức tạp trong khoa học, kỹ thuật và kinh tế, hiểu biết về độ dốc mở ra một cách nhìn sâu sắc hơn về thế giới xung quanh. Bằng cách nắm vững cách tính (Rise over Run, công thức m = (y2-y1)/(x2-x1)) và phân biệt rõ ràng các loại độ dốc (dương, âm, bằng không, không xác định), bạn đã trang bị cho mình một công cụ phân tích quan trọng. Hy vọng bài viết này đã cung cấp cho bạn cái nhìn tổng quan, dễ hiểu và đầy đủ về khái niệm độ dốc, giúp bạn tự tin áp dụng nó vào học tập và cuộc sống.

