Bạn đã bao giờ tự hỏi tại sao một số đường thẳng lại có “độ dốc không xác định” (undefined slope)? Khái niệm này nghe có vẻ bí ẩn, nhưng thực ra lại ẩn chứa một logic toán học vô cùng thú vị. Bài viết này sẽ đưa bạn vào hành trình khám phá “undefined slope”, từ định nghĩa cơ bản đến những ứng dụng thực tế, giúp bạn hiểu rõ hơn về thế giới của những đường thẳng đứng.
Mục Lục
- Độ Dốc (Slope) Là Gì?
- Giải Mã “Undefined Slope”
- Phương Trình Của Đường Thẳng Đứng
- Ví Dụ Minh Họa
- Ứng Dụng Thực Tế
- Kết Luận
1. Độ Dốc (Slope) Là Gì?
Trước khi đi sâu vào “undefined slope”, chúng ta cần hiểu rõ khái niệm độ dốc. Độ dốc, hay còn gọi là hệ số góc, của một đường thẳng cho biết mức độ “nghiêng” của đường thẳng đó so với trục hoành (trục x). Nó được tính bằng công thức:
m = (y₂ - y₁) / (x₂ - x₁)
Trong đó:
mlà độ dốc (slope)(x₁, y₁)và(x₂, y₂)là tọa độ của hai điểm bất kỳ trên đường thẳng
Độ dốc có thể là số dương (đường thẳng đi lên từ trái sang phải), số âm (đường thẳng đi xuống từ trái sang phải), hoặc bằng 0 (đường thẳng nằm ngang).
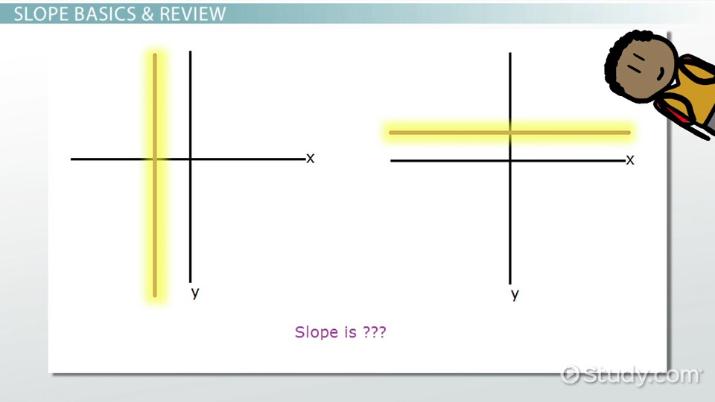
2. Giải Mã “Undefined Slope”
Vậy, “undefined slope” là gì? Đó chính là trường hợp đặc biệt khi mẫu số trong công thức tính độ dốc bằng 0, tức là x₂ - x₁ = 0. Điều này xảy ra khi hai điểm trên đường thẳng có cùng hoành độ (giá trị x), hay nói cách khác, đó là một đường thẳng đứng.
Khi mẫu số bằng 0, phép chia trở nên không xác định trong toán học. Do đó, ta nói đường thẳng đứng có độ dốc “không xác định” (undefined slope).
Hãy tưởng tượng bạn đang cố gắng leo lên một bức tường hoàn toàn thẳng đứng. Bạn không thể tiến lên phía trước (theo chiều ngang), mà chỉ có thể leo lên theo chiều dọc. Độ dốc trong trường hợp này là vô hạn, không thể đo lường được bằng một con số cụ thể.
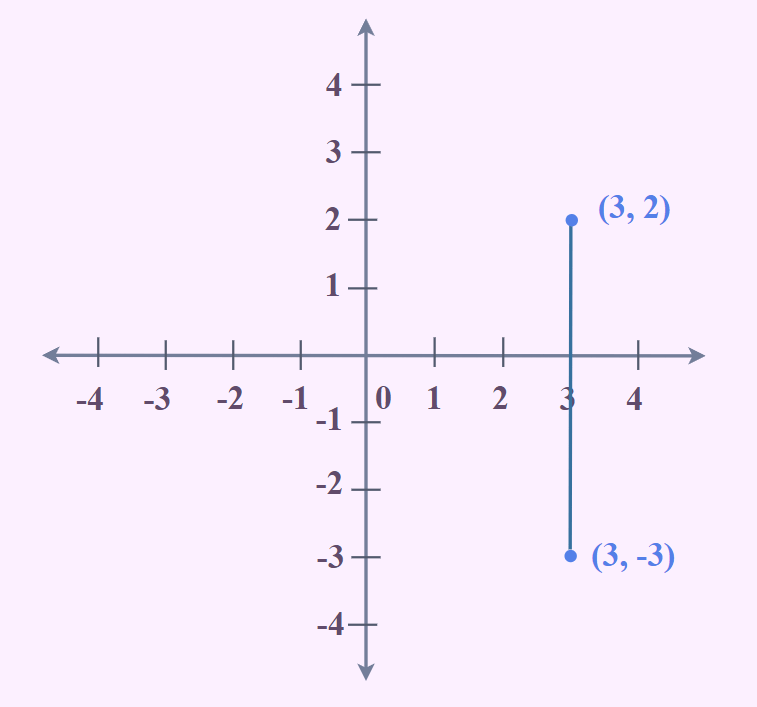
3. Phương Trình Của Đường Thẳng Đứng
Vì đường thẳng đứng không thể được biểu diễn bằng phương trình dạng y = mx + b (trong đó m là độ dốc), chúng ta sử dụng một dạng phương trình khác:
x = c
Trong đó c là một hằng số, chính là hoành độ của mọi điểm trên đường thẳng. Ví dụ, phương trình x = 3 biểu diễn một đường thẳng đứng đi qua tất cả các điểm có hoành độ bằng 3, bất kể tung độ (giá trị y) là bao nhiêu.
4. Ví Dụ Minh Họa
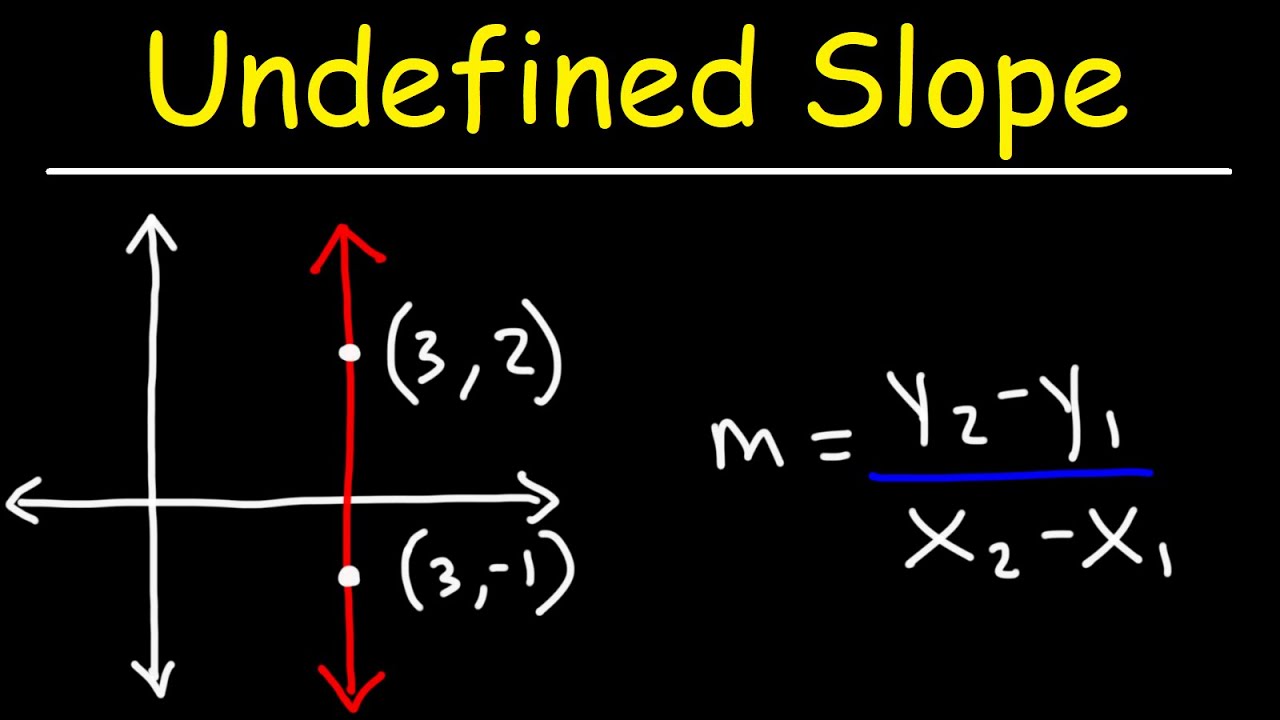
Ví dụ 1: Xét hai điểm A(2, 5) và B(2, 8). Ta có:
x₂ - x₁ = 2 - 2 = 0
Do đó, đường thẳng đi qua hai điểm này có độ dốc không xác định và là một đường thẳng đứng có phương trình x = 2.
Ví dụ 2: Đường thẳng có phương trình x = -1 là một đường thẳng đứng đi qua tất cả các điểm có hoành độ bằng -1.
5. Ứng Dụng Thực Tế
Mặc dù “undefined slope” có vẻ là một khái niệm trừu tượng, nó lại có những ứng dụng thực tế trong:
- Vẽ đồ thị và thiết kế: Hiểu rõ về đường thẳng đứng giúp các nhà thiết kế và họa sĩ tạo ra các bản vẽ kỹ thuật chính xác.
- Xây dựng:Trong xây dựng, các bức tường, cột trụ thường được xây dựng theo phương thẳng đứng, tương ứng với khái niệm độ dốc không xác định.
- Lập trình đồ họa máy tính: Trong đồ họa máy tính, việc xử lý các đường thẳng đứng đòi hỏi các thuật toán riêng biệt, dựa trên đặc điểm độ dốc không xác định của chúng.
- Bản đồ học Các đường kinh tuyến trên bản đồ là các đường thẳng đứng, có độ dốc không xác định.
6. Kết Luận
“Undefined slope” không phải là một khái niệm khó hiểu. Nó đơn giản chỉ ra rằng đường thẳng đó đang “chỉ thẳng lên trời” – một đường thẳng đứng. Việc nắm vững khái niệm này không chỉ giúp bạn giải quyết các bài toán hình học, mà còn mở ra những hiểu biết sâu sắc hơn về thế giới xung quanh, nơi mà những đường thẳng đứng hiện diện ở khắp mọi nơi, từ những tòa nhà chọc trời đến những đường kinh tuyến trên bản đồ.

