Bạn đã bao giờ nghe đến khái niệm “slope” chưa? Nghe có vẻ như một thuật ngữ toán học khô khan, nhưng thực tế, slope lại ẩn chứa nhiều điều thú vị và có ứng dụng rộng rãi hơn bạn nghĩ. Hãy cùng tôi khám phá và giải mã khái niệm này, từ những định nghĩa cơ bản đến các ứng dụng thực tế trong cuộc sống.
1. Slope Là Gì? Định Nghĩa Cơ Bản
Trong toán học, slope (độ dốc) của một đường thẳng là thước đo độ “nghiêng” của đường thẳng đó so với trục hoành (trục x). Nó cho biết sự thay đổi của tung độ (trục y) khi hoành độ thay đổi một đơn vị. Nói cách khác, slope thể hiện “tốc độ” thay đổi của đường thẳng.
Công thức tính slope (thường được ký hiệu là m) giữa hai điểm (x₁, y₁) và (x₂, y₂) trên một đường thẳng là:
m = (y₂ - y₁) / (x₂ - x₁)Giá trị của slope có thể là số dương, số âm, bằng 0 hoặc không xác định.
2. Tìm Hiểu Về Các Loại Slope
Slope có bốn loại chính, mỗi loại có một ý nghĩa và đặc điểm riêng:
- Slope dương (Positive Slope): Đường thẳng đi lên từ trái qua phải. Khi x tăng, y cũng tăng.
- Slope âm (Negative Slope): Đường thẳng đi xuống từ trái qua phải. Khi x tăng, y giảm.
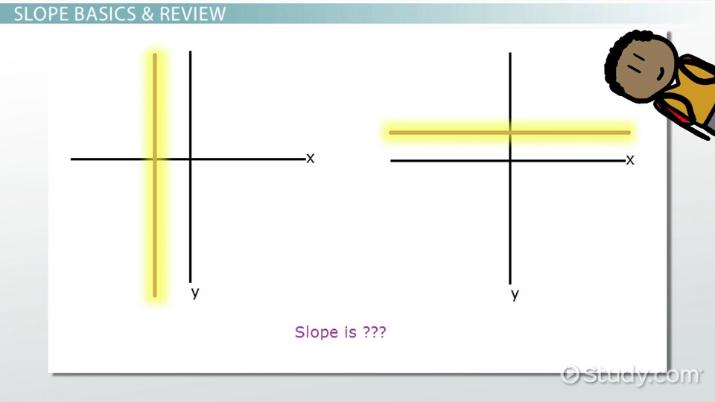
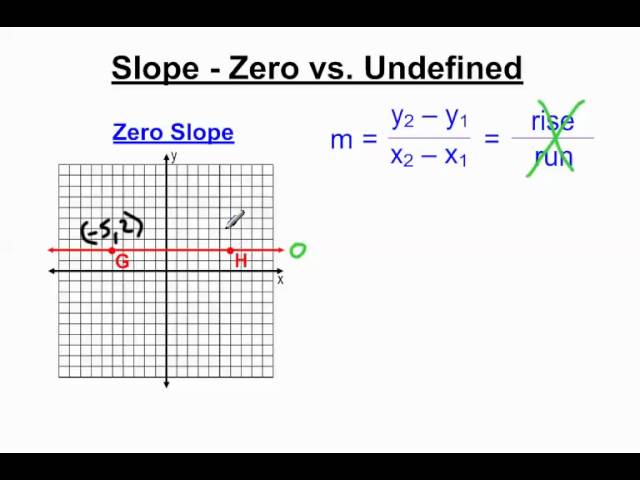
- Slope bằng 0 (Zero Slope): Đường thẳng nằm ngang, song song với trục hoành. Giá trị của y không thay đổi khi x thay đổi.
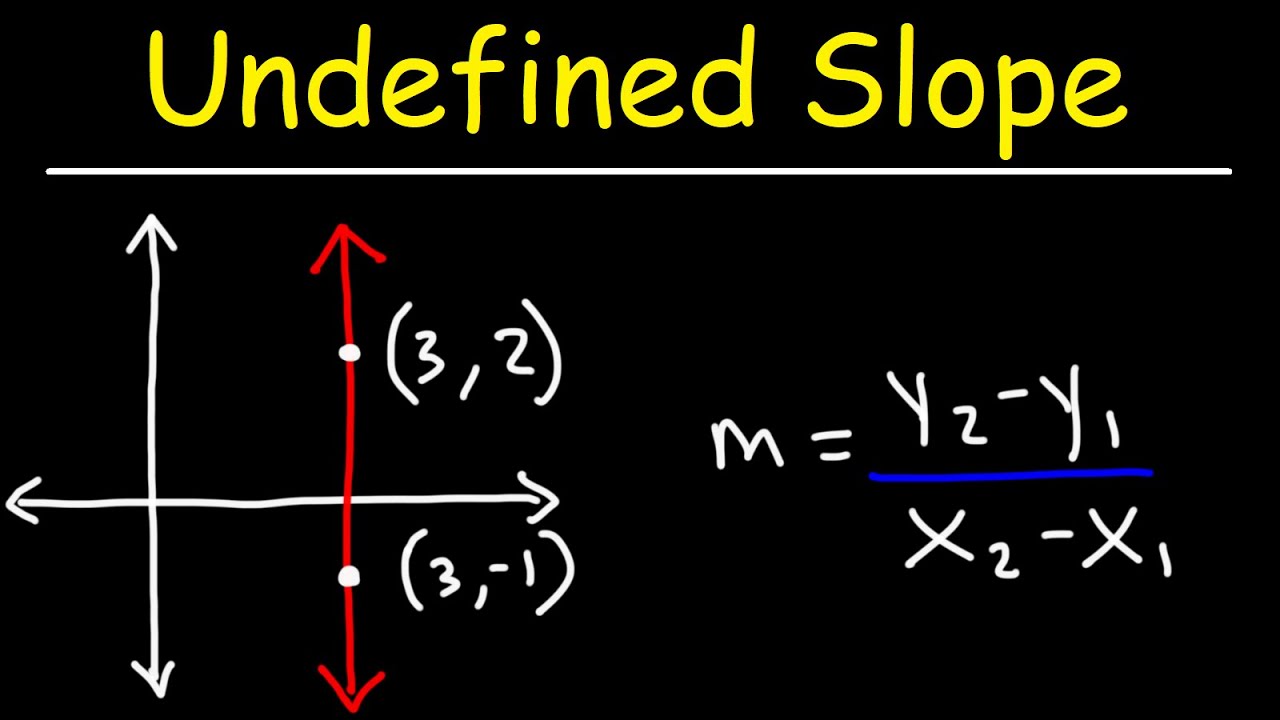
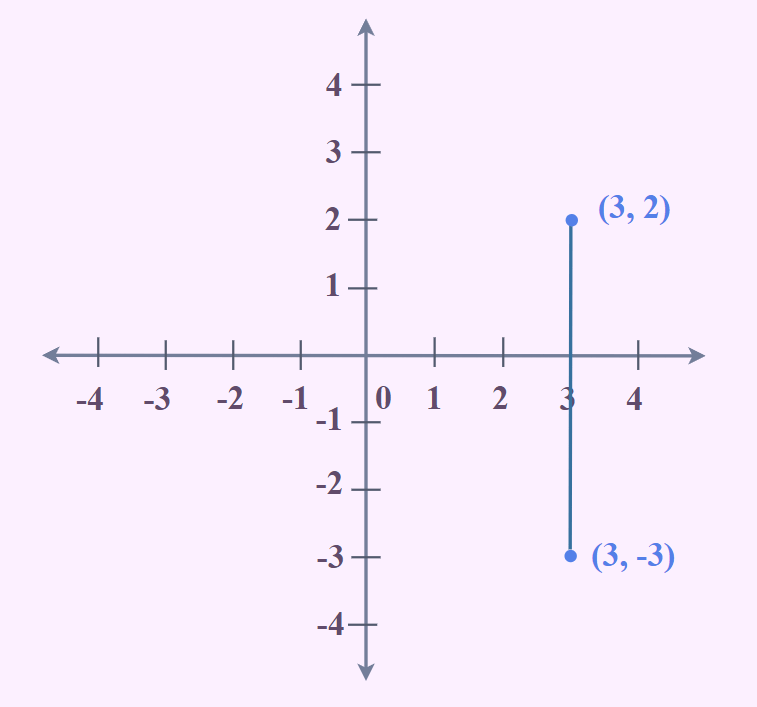
- Slope không xác định (Undefined Slope): Đường thẳng thẳng đứng, song song với trục tung. Giá trị của x không thay đổi, trong khi y có thể là bất kỳ giá trị nào.

3. Ứng Dụng Thực Tế Của Slope
Slope không chỉ là một khái niệm toán học trừu tượng. Nó có mặt ở khắp mọi nơi trong cuộc sống của chúng ta:
- Xây dựng: Độ dốc của mái nhà, đường dốc cho người khuyết tật, độ dốc của đường ống thoát nước… tất cả đều cần tính toán slope để đảm bảo an toàn và hiệu quả.
- Giao thông: Độ dốc của đường, cầu, đường hầm… ảnh hưởng đến tốc độ và khả năng di chuyển của các phương tiện.
- Địa lý: Slope của sườn đồi, núi, sông… giúp các nhà địa chất học hiểu rõ hơn về địa hình và quá trình hình thành của chúng.
- Thiết kế đồ họa: Slope được sử dụng để tạo ra các đường thẳng, đường cong và hình dạng khác nhau trong các phần mềm đồ họa.
- Kinh Tế Học: Thể hiện qua đường cung và đường cầu.
- Khoa học máy tính: Rất nhiều các giải thuật trong học máy (machine learning) sử dụng slope để tìm các điểm cực trị.
4. Tổng Kết: Hiểu Rõ Slope, Mở Rộng Tư Duy
Slope, từ một khái niệm toán học cơ bản, đã mở ra một thế giới ứng dụng rộng lớn. Việc hiểu rõ về slope không chỉ giúp chúng ta giải quyết các bài toán, mà còn giúp chúng ta có một cái nhìn sâu sắc hơn về thế giới xung quanh. Từ những công trình kiến trúc hùng vĩ đến những con đường quen thuộc, slope luôn hiện diện và đóng một vai trò quan trọng. Vì vậy, hãy trân trọng những kiến thức tưởng chừng như đơn giản này, bởi chúng có thể mang lại những giá trị không ngờ.

