Bạn đã bao giờ nghe đến khái niệm “slope” chưa? Nghe có vẻ “toán học” quá phải không? Đừng lo, bài viết này sẽ “giải mã” slope một cách dễ hiểu nhất, đồng thời khám phá những ứng dụng thú vị của nó trong đời sống, vượt xa phạm vi lớp học toán.
1. Slope là gì? Định nghĩa và ý nghĩa
Slope, hay còn gọi là độ dốc, là một khái niệm toán học mô tả độ nghiêng của một đường thẳng so với trục hoành (trục x) trong hệ tọa độ Descartes. Nó cho biết mức độ thay đổi của tung độ (trục y) khi hoành độ (trục x) thay đổi một đơn vị. Nói một cách đơn giản, slope càng lớn thì đường thẳng càng “dốc”.
Slope không chỉ là một con số trừu tượng. Nó mang ý nghĩa quan trọng trong việc biểu diễn sự thay đổi, tốc độ biến thiên, và mối quan hệ giữa hai đại lượng. Slope giúp chúng ta hình dung và phân tích các đường thẳng, từ đó hiểu rõ hơn về các hiện tượng trong thế giới thực.
2. Các dạng Slope thường gặp
Slope có thể có nhiều giá trị khác nhau, và mỗi giá trị lại biểu thị một dạng đường thẳng khác nhau. Cùng tìm hiểu các dạng slope phổ biến:
2.1. Slope dương
Khi slope có giá trị dương, đường thẳng sẽ “đi lên” từ trái sang phải. Điều này có nghĩa là khi giá trị x tăng thì giá trị y cũng tăng theo. Ví dụ, đồ thị biểu diễn mối quan hệ giữa thời gian học và điểm số thường có slope dương (học càng nhiều, điểm càng cao).
2.2. Slope âm
Ngược lại với slope dương, slope âm biểu thị một đường thẳng “đi xuống” từ trái sang phải. Khi giá trị x tăng, giá trị y giảm. Chẳng hạn, đồ thị biểu diễn mối quan hệ giữa số lượng hàng tồn kho và lợi nhuận có thể có slope âm (càng nhiều hàng tồn kho, lợi nhuận càng giảm).
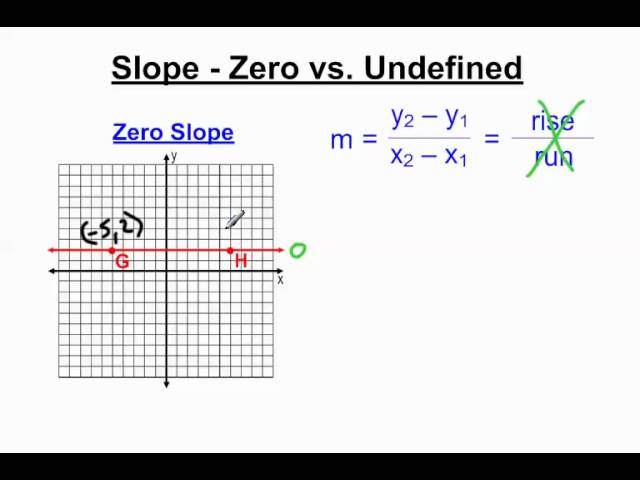
2.3. Slope bằng 0
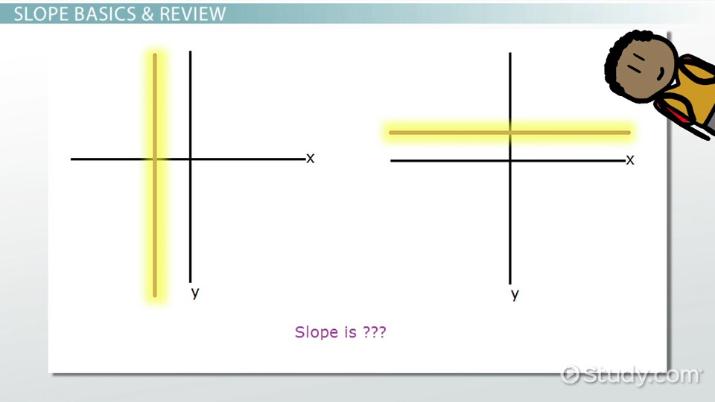
Một đường thẳng nằm ngang song song với trục hoành sẽ có slope bằng 0. Điều này cho thấy giá trị y không thay đổi bất kể giá trị x thay đổi như thế nào. Ví dụ, mực nước biển (nếu bỏ qua thủy triều) có thể được xem là một đường thẳng có slope bằng 0.

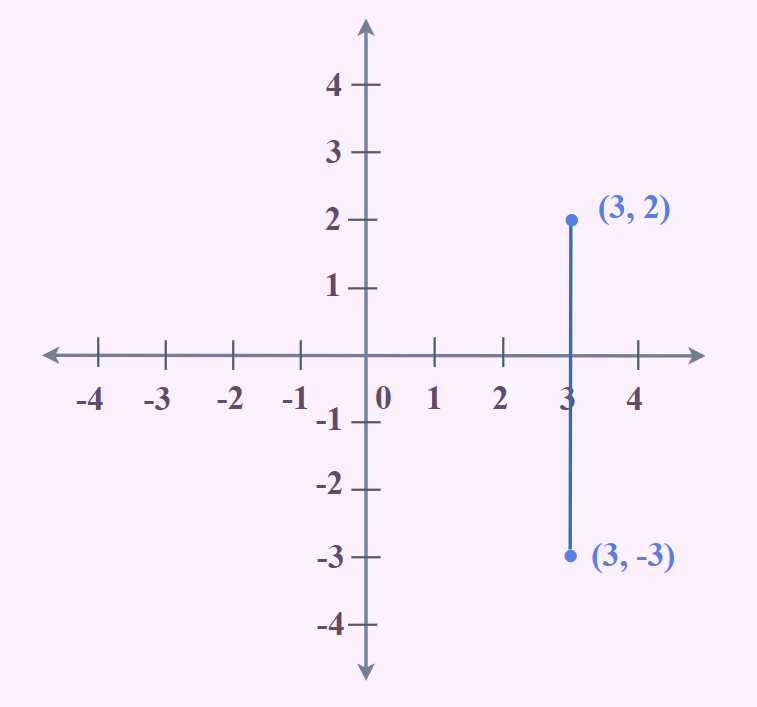
2.4. Slope không xác định
Một đường thẳng đứng song song với trục tung sẽ có slope không xác định. Lý do là vì không có sự thay đổi nào trong giá trị x, nhưng lại có sự thay đổi vô hạn trong giá trị y. Việc chia cho 0 (sự thay đổi của x) là không xác định trong toán học.
3. Công thức tính Slope
Để “cụ thể hóa” slope, chúng ta cần công thức tính toán. Có hai cách chính để xác định slope:
3.1. Tính Slope khi biết hai điểm
Nếu biết tọa độ của hai điểm trên đường thẳng, (x₁, y₁) và (x₂, y₂), công thức tính slope (thường ký hiệu là m) là:
m = (y₂ – y₁) / (x₂ – x₁)
Đây là công thức cơ bản và quan trọng nhất để tính slope. Nó thể hiện rõ ý nghĩa của slope là tỷ lệ thay đổi giữa tung độ và hoành độ.
3.2. Tính Slope từ phương trình đường thẳng
Nếu có phương trình đường thẳng dạng y = mx + b, thì m chính là slope của đường thẳng đó. Hằng số b là tung độ gốc (y-intercept), là điểm mà đường thẳng cắt trục y.
4. Ứng dụng của Slope trong thực tế
Slope không chỉ giới hạn trong sách giáo khoa toán. Nó có mặt trong rất nhiều lĩnh vực của cuộc sống, mang lại những ứng dụng thiết thực:
4.1. Trong xây dựng
Độ dốc của mái nhà, đường ống thoát nước, đường dốc cho người khuyết tật… đều là những ứng dụng quan trọng của slope. Việc tính toán slope chính xác đảm bảo tính an toàn, thẩm mỹ và công năng của công trình.
4.2. Trong thiết kế đồ họa
Slope được sử dụng để vẽ các đường thẳng, tạo hình khối, và thiết kế các đối tượng trong không gian hai chiều và ba chiều.
4.3. Trong địa lý và bản đồ học
Độ dốc của địa hình, độ nghiêng của sườn núi, dòng chảy của sông suối… đều được biểu diễn và phân tích bằng slope. Slope giúp các nhà địa lý hiểu rõ hơn về đặc điểm tự nhiên và quy luật vận động của Trái Đất.
4.4. Trong tài chính
Slope có thể được sử dụng để biểu diễn tốc độ tăng trưởng của doanh thu, lợi nhuận, hoặc giá cổ phiếu. Nó giúp các nhà đầu tư phân tích xu hướng và đưa ra quyết định đầu tư.
5. Slope và các khái niệm liên quan
Để hiểu sâu hơn về slope, chúng ta cần xem xét mối liên hệ của nó với một số khái niệm khác:
5.1. Góc nghiêng (Angle of Inclination)
Góc nghiêng là góc tạo bởi đường thẳng và trục hoành. Slope và góc nghiêng có mối quan hệ chặt chẽ với nhau thông qua hàm tang. Cụ thể, slope bằng tang của góc nghiêng.
5.2. Hệ số góc (Gradient)
Trong một số ngữ cảnh, đặc biệt là trong giải tích vector, “gradient” được dùng thay cho “slope” để chỉ độ dốc của một hàm số nhiều biến. Gradient không chỉ cho biết độ dốc mà còn cho biết hướng mà hàm số tăng nhanh nhất.
6. Kết luận
Slope, từ một khái niệm toán học cơ bản, đã “vượt rào” ra khỏi trang giấy để đi vào cuộc sống một cách tự nhiên và hữu ích. Hy vọng bài viết này đã giúp bạn “thân thiện” hơn với slope, hiểu rõ hơn về ý nghĩa và ứng dụng của nó. Đừng ngại “khám phá” slope trong những tình huống thực tế, bạn sẽ thấy nó thú vị hơn bạn tưởng đấy!

