Bạn đã bao giờ đối mặt với khái niệm “undefined slope” (độ dốc không xác định) trong toán học và cảm thấy bối rối? Đừng lo lắng, bạn không hề đơn độc! Bài viết này sẽ giúp bạn “giải mã” bí ẩn đằng sau đường thẳng đứng và độ dốc “không xác định” của nó, đồng thời khám phá những ứng dụng thú vị của khái niệm này trong thực tế.
1. “Undefined Slope” (Độ Dốc Không Xác Định) – Khái Niệm Gây Hoang Mang
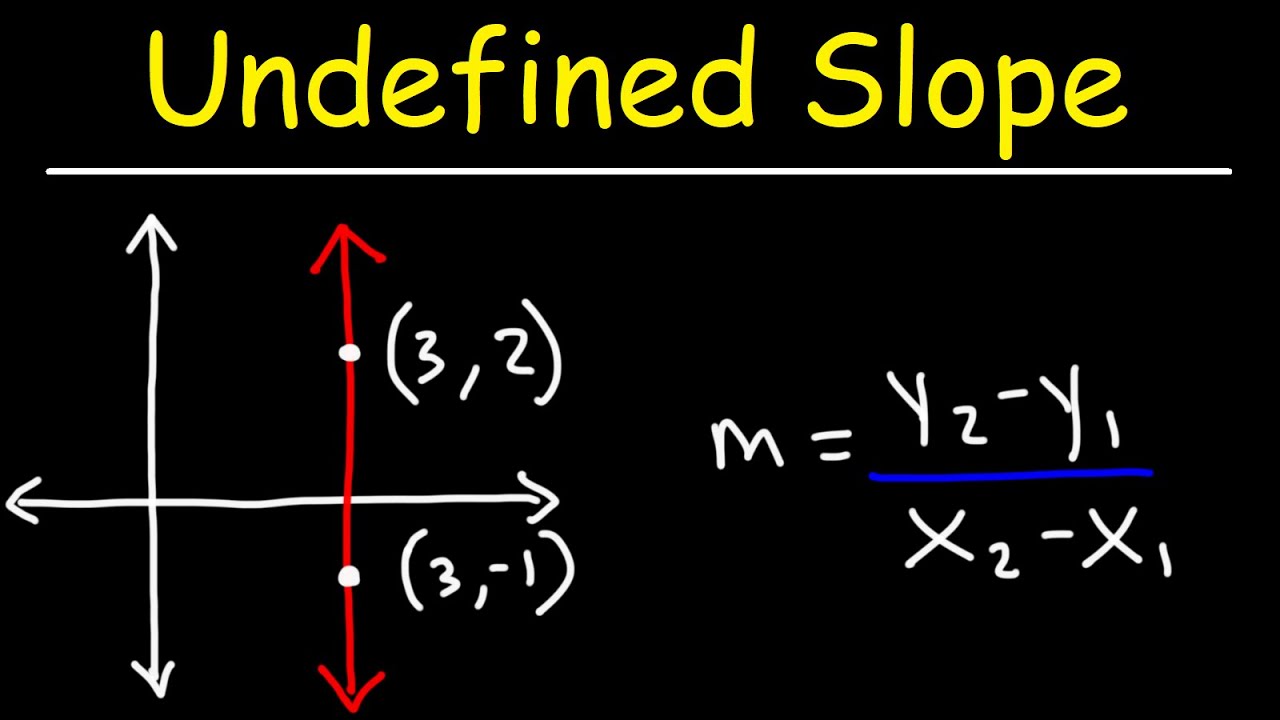
Trong hệ tọa độ Descartes quen thuộc, độ dốc (slope) của một đường thẳng được định nghĩa là sự thay đổi tung độ (y) chia cho sự thay đổi hoành độ (x) giữa hai điểm bất kỳ trên đường thẳng đó. Công thức tính độ dốc thường được biểu diễn như sau:
m = (y2 - y1) / (x2 - x1)Trong đó:
mlà độ dốc (slope)(x1, y1)và(x2, y2)là tọa độ của hai điểm trên đường thẳng
Tuy nhiên, khi áp dụng công thức này cho một đường thẳng đứng, chúng ta gặp phải một vấn đề “nan giải”: Mẫu số (x2 – x1) bằng 0, dẫn đến phép chia cho 0 – một phép toán không xác định trong toán học. Đây chính là lý do tại sao đường thẳng đứng có “undefined slope”.
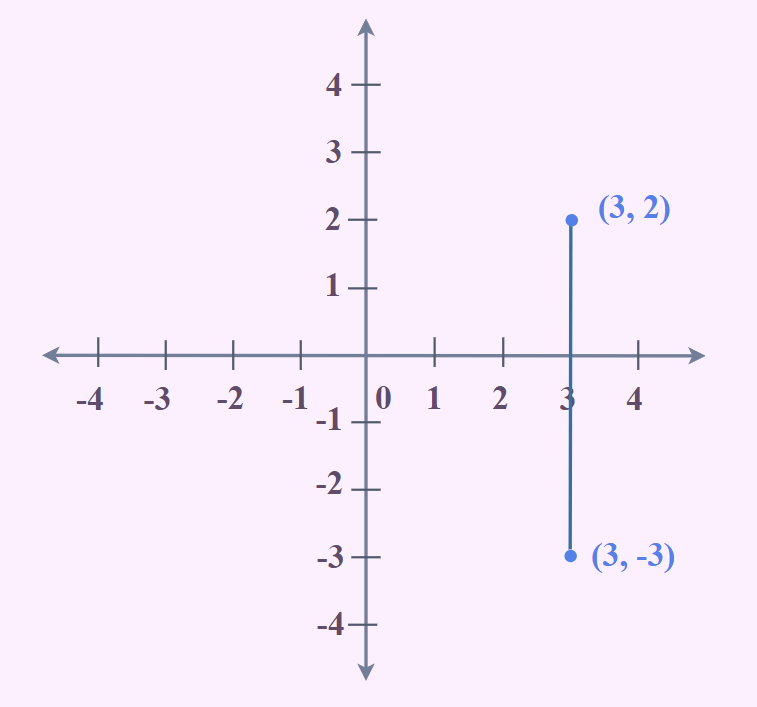
2. Tại Sao Đường Thẳng Đứng Lại Có “Undefined Slope”?
Để hiểu rõ hơn, hãy tưởng tượng bạn đang leo lên một ngọn đồi. Độ dốc của ngọn đồi cho biết mức độ “dốc” của nó – ngọn đồi càng dốc, độ dốc càng lớn. Bây giờ, hãy hình dung bạn đang cố gắng leo lên một bức tường thẳng đứng. Bạn có thể leo lên được không? Không, vì bức tường không có độ “nghiêng” nào cả. Nó hoàn toàn thẳng đứng!
Tương tự như vậy, đường thẳng đứng không có sự thay đổi nào về hoành độ (x). Bất kể bạn chọn hai điểm nào trên đường thẳng, giá trị x luôn không đổi. Điều này dẫn đến việc mẫu số trong công thức tính độ dốc bằng 0, và do đó, độ dốc trở thành “không xác định”.
3. Phân Biệt “Undefined Slope” và “Zero Slope”
Một lỗi phổ biến là nhầm lẫn giữa “undefined slope” và “zero slope” (độ dốc bằng 0). “Zero slope” xảy ra với các đường thẳng nằm ngang. Trên những đường thẳng này, giá trị tung độ (y) không thay đổi, dẫn đến tử số trong công thức tính độ dốc bằng 0, và do đó, độ dốc bằng 0.
- Đường thẳng đứng: “Undefined slope” (Độ dốc không xác định).
- Đường thẳng nằm ngang: “Zero slope” (Độ dốc bằng 0).

4. Ứng Dụng Thực Tế Của Việc Hiểu “Undefined Slope”
Khái niệm “Undefined Slope” không chỉ là một câu đố trong toán học trừu tượng mà nó còn có những ứng dụng rất thực tế:
- Lập trình đồ họa máy tính: Trong đồ họa máy tính, việc hiểu rõ về các đường thẳng và độ dốc của chúng là rất quan trọng để vẽ và hiển thị các đối tượng trên màn hình.
- Xây dựng và kiến trúc: Các bức tường, cột trụ và nhiều yếu tố kiến trúc khác là những ví dụ điển hình về “đường thẳng đứng” và được ứng dụng trong thực tế.
- Phân tích dữ liệu: Trong một số trường hợp, “undefined slope” có thể xuất hiện trong quá trình phân tích dữ liệu, đòi hỏi người phân tích phải có cách xử lý phù hợp.
- Vật lý: Trong một số trường hợp khi ta xét thời gian chuyển động của một vật bằng 0, với quãng đường khác 0 thì vận tốc cũng không xác định.
5. “Undefined Slope” Trong Các Hệ Toạ Độ Khác
Mặc dù “undefined slope” thường được thảo luận trong bối cảnh hệ tọa độ Descartes, khái niệm này cũng có thể mở rộng sang các hệ tọa độ khác. Ví dụ, trong hệ tọa độ cực, một đường thẳng đi qua gốc tọa độ và tạo với trục cực một góc không đổi sẽ có độ dốc không xác định khi góc đó là π/2 (90 độ) hoặc 3π/2 (270 độ).

6. Kết Luận: Chinh Phục Khái Niệm “Undefined Slope”
Như vậy, “undefined slope” không phải là một khái niệm quá đáng sợ, phải không nào? Thực tế thì việc hiểu rõ về “Undefined Slope” chính là chìa khóa giúp mở ra những bài toán “hóc búa” về phương trình đường thẳng, cũng như ứng dụng kiến thức này trong thực tế. Hy vọng qua bài viết này giúp bạn tiếp cận gần hơn với khái niệm “Undefined Slope”, cũng như hiểu hơn về các ứng dụng thực tế của nó nhé!

