1. Mở Đầu: Độ Dốc – Khái Niệm Vượt Ra Ngoài Trang Giấy
Bạn đã bao giờ leo dốc, trượt tuyết, hay đơn giản là ngắm nhìn một con đường uốn lượn? Nếu có, bạn đã trực tiếp trải nghiệm khái niệm “độ dốc” – một yếu tố quan trọng không chỉ trong toán học mà còn trong vô số khía cạnh của cuộc sống. Bài viết này sẽ đưa bạn vào một hành trình khám phá độ dốc, từ những định nghĩa cơ bản đến những ứng dụng bất ngờ, giúp bạn “giải mã” khái niệm tưởng chừng như đơn giản này.
2. Độ Dốc Trong Toán Học: Nền Tảng Và Ứng Dụng
2.1. Khái Niệm Cơ Bản Về Độ Dốc
Trong toán học, độ dốc (slope) của một đường thẳng là thước đo độ “nghiêng” của đường thẳng đó so với trục hoành. Nó được định nghĩa là sự thay đổi theo chiều dọc (trục tung) chia cho sự thay đổi theo chiều ngang (trục hoành) giữa hai điểm bất kỳ trên đường thẳng.
Công thức tính độ dốc (m) thường được biểu diễn như sau:
m = (y₂ – y₁) / (x₂ – x₁)
Trong đó (x₁, y₁) và (x₂, y₂) là tọa độ của hai điểm trên đường thẳng.
2.2. Các Dạng Độ Dốc Thường Gặp
2.2.1. Độ Dốc Dương
Khi đường thẳng đi lên từ trái sang phải, độ dốc sẽ dương (m > 0). Điều này có nghĩa là khi giá trị x tăng thì giá trị y cũng tăng.
2.2.2. Độ Dốc Âm
Khi đường thẳng đi xuống từ trái sang phải, độ dốc sẽ âm (m < 0). Điều này có nghĩa là khi giá trị x tăng thì giá trị y giảm.

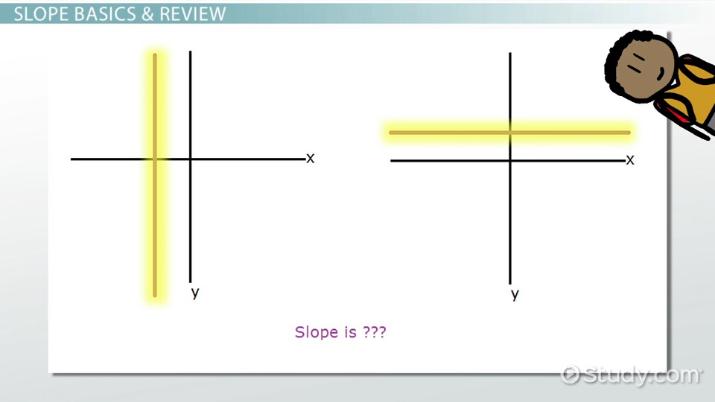
2.2.3. Độ Dốc Bằng Không
Đường thẳng nằm ngang có độ dốc bằng không (m = 0). Điều này có nghĩa là giá trị y không thay đổi khi giá trị x thay đổi.

2.2.4. Độ Dốc Không Xác Định
Đường thẳng thẳng đứng có độ dốc không xác định. Điều này xảy ra vì sự thay đổi theo chiều ngang bằng không (x₂ – x₁ = 0), dẫn đến việc chia cho 0 trong công thức tính độ dốc.

2.3. Ứng Dụng Của Độ Dốc Trong Toán Học
- Đại số: Tìm phương trình đường thẳng, xác định tính song song và vuông góc của hai đường thẳng.
- Giải tích: Tính đạo hàm (độ dốc của tiếp tuyến), tìm cực trị của hàm số.
- Hình học: Xác định góc giữa hai đường thẳng các bài toán liên quan không gian, vecto.
3. Độ Dốc Trong Thực Tế: Từ Đường Đèo Đến Tài Chính
3.1. Địa Hình Và Xây Dựng
Độ dốc của địa hình tự nhiên (đồi núi, thung lũng) ảnh hưởng đến việc quy hoạch đô thị, thiết kế công trình xây dựng (nhà ở, cầu đường, đập nước…). Các kỹ sư phải tính toán độ dốc để đảm bảo tính ổn định, an toàn và thẩm mỹ của công trình.
3.2. Giao Thông Vận Tải
Độ dốc của đường sá ảnh hưởng lớn đến tốc độ, khả năng vận hành của phương tiện giao thông, và thiết kế các biển báo an toàn.
3.3. Tài Chính Và Kinh Tế
Trong kinh tế, độ dốc của đường cung và đường cầu thể hiện mối quan hệ giữa giá cả và lượng cung/cầu của một sản phẩm. Độ dốc của đường cong biểu đồ chứng khoán thể hiện xu hướng tăng/giảm giá.
3.4. Khoa Học Và Kỹ Thuật
Độ dốc xuất hiện trong nhiều lĩnh vực khoa học và kỹ thuật khác nhau. Ví dụ, trong vật lý, độ dốc của đồ thị biểu diễn mối quan hệ giữa vận tốc và thời gian chính là gia tốc.
4. “Chinh Phục” Độ Dốc: Mẹo Nhỏ Cho Học Sinh, Sinh Viên
- Nắm vững công thức: Hiểu rõ bản chất và cách áp dụng công thức tính độ dốc.
- Luyện tập thường xuyên: Giải nhiều bài tập với các dạng độ dốc khác nhau để làm quen và thành thạo.
- Liên hệ thực tế: Tìm kiếm các ví dụ về độ dốc trong cuộc sống để tăng hứng thú và hiểu sâu hơn về khái niệm này.
- Sử dụng công cụ hỗ trợ : Sử dụng các phần mềm, trang web vẽ đồ thị để minh họa và kiểm tra kết quả.
5. Kết Luận: Ý Nghĩa Triết Học Của Độ Dốc
Độ dốc không chỉ là một khái niệm toán học khô khan mà còn mang ý nghĩa triết học sâu sắc. Nó tượng trưng cho sự thay đổi, thử thách và những nỗ lực để vượt qua khó khăn. Giống như việc leo lên một con dốc, cuộc sống đòi hỏi chúng ta phải không ngừng tiến lên, đối mặt với những trở ngại và “chinh phục” những đỉnh cao mới.

